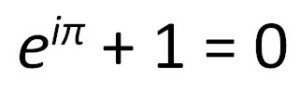Нееуклидске геометрије
Геометрија коју је свако од нас учио или учи у школи јесте еуклидска геометрија. То је геометрија која се, поред осталих аксиома, заснива на аксиоми (постулату) паралелности. Име је добила по античком математичару Еуклиду, аутору књиге „Елементи“, у којој је објединио сва дотадашња знања из геометрије.
Постулат паралелности у еуклидској геометрији је еквивалентан тврђењу да, у дводимензионом простору, за произвољну праву l и тачку P која јој не припада, постоји тачно једна права која садржи P и не сече праву l, односно која је паралелна са l.
Математичари су се дуго мучили да докажу такву теорему, али им није полазило за руком, па су одлучили да је усвоје као аксиому. Међутим, некима од њих прошло је кроз главу: „Толико се мучимо да је докажемо, и не успевамо, шта ако уствари није тачна?“ Одатле креће развој нових геометрија…
„Главни кандидати“ који би засенили славу еуклидске геометрије биле су елиптичка и хиперболичка геометрија.
Неколико стотина година, геометри (математичари) су се мучили око сложености петог постулата, верујући да се он може доказати као теорема изведена из остала четири постулата. Многи су покушавали да пронађу доказ заснован на методу свођења на противуречност. Међу њима је најпознатији био Италијан Ђовани Сакери. У раду насловљеном „Еуцлидес аб Омни Наево Виндицатус“ (Еуклид ослобођен од свих грешака), објављеном 1733, он одмах одбацује елиптичку геометрију као могућност (неке од осталих Еуклидових аксиома морале би бити модификоване да би елиптичка геометрија функционисала) и баца се на посао доказујући велики број резултата у хиперболичкој геометрији. Његова коначна поента је у томе да ови резултати који су у супротности са теоремама еуклидске геометрије доказују немогућност хиперболичке геометрије. Међутим, никакве логичке противуречности унутар ових резултата није било. Тако покушавајући да докаже Еуклидову геометрију он уместо тога у ствари ненамерно открива једну нову геометрију света. Ипак у то време још увек је широко било распрострањено веровање да наш свет или универзум функционише у складу са принципима еуклидске геометрије.
Сто година касније, тачније 1829. године, Рус Николај Иванович Лобачевски објављује студију о хиперболичкој геометрији. Из тог разлога, хиперболичка геометрија се често назива и „геометрија Лобачевског“. Отприлике у исто време, Мађар Јанош Бољаји такође пише своју студију о хиперболичкој геометрији, коју објављује 1832. као додатак на један рад свог оца. Велики математичар Карл Фридрих Гаус чита овај додатак и одговара Бољајију да је од до истих резултата и он лично дошао нешто раније.
Међутим приоритет у овом открићу припао је Лобачевском због ранијег објављивања свог рада. Основна разлика између овог и ранијих радова, као што је Сакеријев, је у томе што он први без икакве сумње тврди да Еуклидова геометрија није једина могућа геометрија, нити је једина опажајна структура нашег Универзума. Лобачевски назива еуклидску геометрију „обичном геометријом“, а своју нову хиперболичку геометрију „имагинарном геометријом“. Ипак, још увек се задржала могућност да су аксиоми хиперболичке геометрије логички некозистентни. Као што он напомиње, још доста посла требало би да буде урађено да би се потпуније засновала елиптичка геометрија.
Бернхард Риман, у својој чувеној лекцији из 1854, заснива област Риманове геометрије, разматрајући посебно идеје које се сада називају многострукост, Риманова метрика, и закривљеност. Он конструише бесконачну фамилију нееуклидских геометрија задајући овој фамилији формулу Риманове метрике на јединичној лопти у еуклидском простору. Понекад је њему неправедно приписивана част да је једини откривач елиптичне геометрије; али у ствари, ова његова конструкција показује далековидост његовог рада и чињеницу да су његове теореме важеће за све врсте геометрија.
Уобичајени модел за еуклидску геометрију је „равна површ“. С друге стране, најједноставњији модел за елиптичку геометрију је сфера, где су праве линије (нееуклидске праве) „велике кружнице“ (такве као што су екватор или меридијани на глобусу), док се тачке супротне једна другој подударају (сматрају се истим тачкама).
Чак и након радова Лобачевског, Гауса и Бољајиа, остало је питање: Да ли постоји модел очигледног представљања хиперболичке геометрије? На ово питање одговорио је Еугенио Белтрами, 1868, који је показао да површина названа псеудосфера има одговарајућу закривљеност за један модел делимичног хиперболичког простора, а у другом чланку објављеном исте године, дефинисан је Клајнов модел (Феликс Клајн), Поенкареов диск модел и Поенкареов полуравански модел (Анри Поенкаре) који чине у потпуности моделе очигледног представљања хиперболичке геометрије, а уједно показују да су еуклидска геометрија и хиперболичка геометрија еквиконзистентне, што значи да је хиперболичка геометрија логички конзистентна уколико је то и еуклидска геометрија. (Обрнута импликација следи из хоросферског модела еуклидске геометрије)
Развој нееуклидских геометрија показао се веома значајним за физику 20. века. Задајући ограничења брзини светлости, сабирање брзина захтевало је нужно коришћење хиперболичке геометрије. Ајнштајнова Општа теорија релативности описује простор као генерално раван (еуклидски), али и елиптички закривљен (нееуклидски) у областима у близини којих је присутна материја. С обзиром да се васиона шири (погледати чланак Хаблов закон), чак и простор где не постоји материја или маса може се описивати уз помоћ хиперболичког модела. Ова врста геометрије, где се закривљеност мења од тачке до тачке названа је римановска геометрија.
Постоје такође и други математички модели површи на којима Еуклидов постулат паралелности више не важи, као на пример Денова површ која се састоји од свих тачака (x, y), где су x и y коначни надреални бројеви.
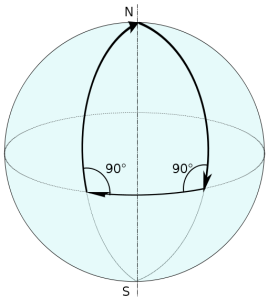
У сферној геометрији, на површини сфере нема паралелних линије.
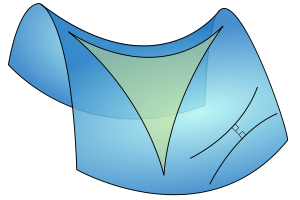
Троугао и две паралелне праве на седластој равни (хиперболички параболоид).
Извор: Википедија
О НАЈЛЕПШОЈ МАТЕМАТИЧКОЈ ФОРМУЛИ
Славни Ојлеров идентитет вероватно је најелегантнија и најлепша формула у историји математике, и то управо оне коју је харвардски професор Бенџамин Пирс назвао “апсолутно парадоксалном”. Ова формула једна је од неколико стотина блиставих постигнућа Леонарда Ојлера, и симболизује нешто што надмашује границе математике, па и читаве науке, и говори нам нешто о универзалним вредностима сваког истинског људског постигнућа.
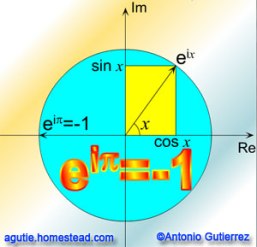
Ојлер је увео употребу експоненцијалне функције и логаритама у аналитичке доказе. Открио је начин да изрази различите логаритамске функције помоћу степених редова, и успешно је дефинисао логаритме негативних и комплексних и на тај начин,проширио домен математичке примене логаритама. Дефинисао је експоненцијалну функцију за комплексне бројеве и открио њену везу са тригонометријским функцијама. За произвољан реалан број фи, према Ојлеровој формули, важи једнакост
Посебан случај те формуле, који се добија за вредност  познат као Ојлеров идентитет,
познат као Ојлеров идентитет,
Одакле потиче њена елеганција? Одговор је: из минималног броја симбола, у којима су обједињене кључне области математике:
е – (реална) анализа
π – геометрија, тригонометрија
i– алгебра, комплексна анализа
0,1 – аритметика .
Читаоци часописа Mathematical Intelligencer су 1988. године овај идентитет прогласили за најлепшу математичку формулу свих времена. Треба рећи да су се међу пет првопласираних формула на том гласању нашле чак три до којих је дошао Ојлер.
Овом формулом ударени су темељи не само комплексне анализе, већ и свих области које се њоме користе, од телекомуникација до квантне теорије поља. Занимљиво је да се све велике формуле у историји науке везују на неочекиван и често шокантан начин различите концепте, и то управо оне који се на први мах чине неспојивим или међусобно искључивим.